Tree structure (construction, traversal)

Trees: Unlike Arrays, Linked Lists, Stack and queues, which are linear data structures, trees are hierarchical data structures.

Tree Vocabulary: The topmost node is called root of the tree. The elements that are directly under an element are called its children. The element directly above something is called its parent. For example, ‘a’ is a child of ‘f’, and ‘f’ is the parent of ‘a’. Finally, elements with no children are called leaves.

Tree is a hierarchical data structure. Main uses of trees include maintaining hierarchical data, providing moderate access and insert/delete operations. Binary trees are special cases of tree where every node has at most two children.

      tree
      ----
       j    <-- root
     /   \
    f      k  
  /   \      \
 a     h      z    <-- leaves

• One reason to use trees might be because you want to store information that naturally forms a hierarchy. For example, the file system on a computer:

file system
-----------
     /    <-- root
  /      \
...       home
      /          \
   ugrad        course
    /       /      |     \
  ...      cs101  cs112  cs113  

• Trees (with some ordering e.g., BST) provide moderate access/search (quicker than Linked List and slower than arrays).

• Trees provide moderate insertion/deletion (quicker than Arrays and slower than Unordered Linked Lists).

• Like Linked Lists and unlike Arrays, Trees don’t have an upper limit on number of nodes as nodes are linked using pointers.

Main applications of trees include:

1. Manipulate hierarchical data.

2. Make information easy to search (see tree traversal).

3. Manipulate sorted lists of data.

4. As a workflow for compositing digital images for visual effects.

5. Router algorithms

6. Form of a multi-stage decision-making (see business chess).

Binary Tree: A tree whose elements have at most 2 children is called a binary tree. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.

Properties

• The maximum number of nodes at level ‘l’ of a binary tree is 2l-1.

• Maximum number of nodes in a binary tree of height ‘h’ is 2h – 1.

• In a Binary Tree with N nodes, minimum possible height or minimum number of levels is Log2(N+1)

• In Binary tree where every node has 0 or 2 children, number of leaf nodes is always one more than nodes with two children.

Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями.

binary-tree-ex

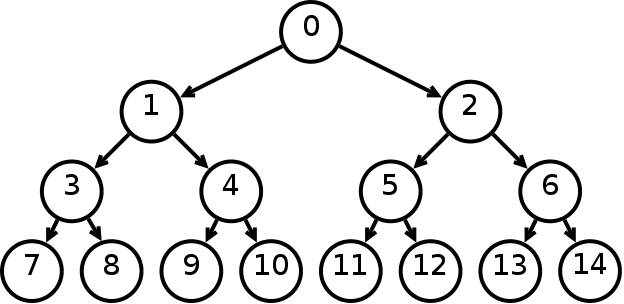
Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом, если равно, то значение найдено и поиск прекращается.

binary-tree-past

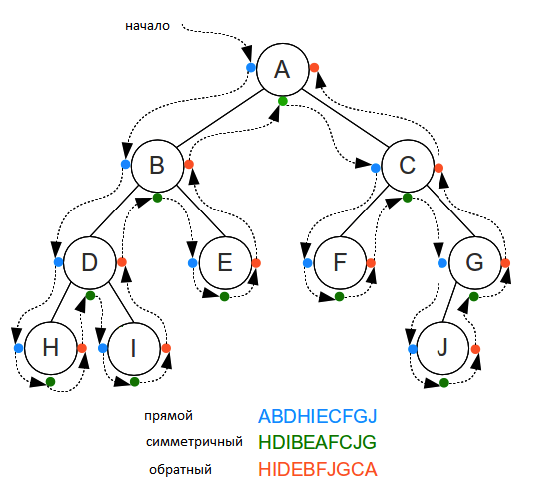
Поиск минимального значения невероятно прост — это всегда самый левый узел, то есть мы пробегаем по всем потомкам, если у потомка есть левый лист, значит бежим по его потомкам. Как только мы видим, что потомков нет — вуаля, у нас самое маленькое значение

binary-min

Тоже самое с самым большим значением — оно всегда самое правое

binary-max

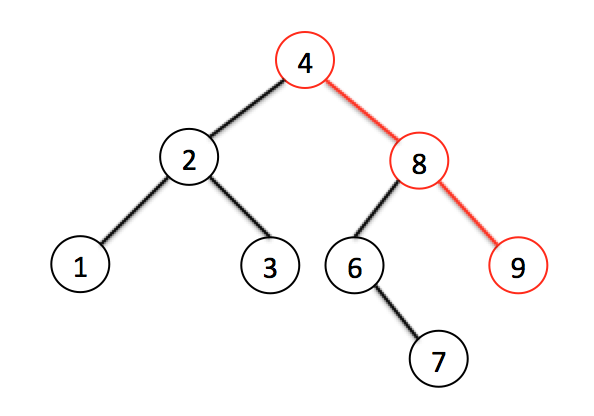
Поиск элемента тоже очень прост:

1. Как обычно начинаем с корневого элемента.

2. Проверяем или даный элемент — тот который нам нужен. Если да — возвращаем

3. и нет: смотрим или он больше даного, или меньше. Идем к соответствующему листу

4. Если листов нет — элемента нет. Если есть — повторяем пункт 2.

Traversals

Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways. Following are the generally used ways for traversing trees.

tree-example

Depth First Traversals:

• (a) Inorder (Left, Root, Right) : 4 2 5 1 3

• (b) Preorder (Root, Left, Right) : 1 2 4 5 3

• (c) Postorder (Left, Right, Root) : 4 5 2 3 1

Breadth First or Level Order Traversal : 1 2 3 4 5

Inorder Traversal (Practice):

Algorithm Inorder(tree)
   1. Traverse the left subtree, i.e., call Inorder(left-subtree)
   2. Visit the root.
   3. Traverse the right subtree, i.e., call Inorder(right-subtree)

In case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal s reversed can be used.

Example: Inorder traversal for the above-given figure is 4 2 5 1 3.

Preorder Traversal (Practice):

Algorithm Preorder(tree)
   1. Visit the root.
   2. Traverse the left subtree, i.e., call Preorder(left-subtree)
   3. Traverse the right subtree, i.e., call Preorder(right-subtree)

Preorder traversal is used to create a copy of the tree. Preorder traversal is also used to get prefix expression on of an expression tree. Example: Preorder traversal for the above given figure is 1 2 4 5 3.

Postorder Traversal (Practice):

Algorithm Postorder(tree)
   1. Traverse the left subtree, i.e., call Postorder(left-subtree)
   2. Traverse the right subtree, i.e., call Postorder(right-subtree)
   3. Visit the root.

Postorder traversal is used to delete the tree. Please see the question for deletion of tree for details. Postorder traversal is also useful to get the postfix expression of an expression tree.

Example: Postorder traversal for the above given figure is 4 5 2 3 1.